Instant run-away-from-this voting system

The rumor is that the Liberal Party of Canada has just voted in caucus to support a switch to instant runoff voting (IRV). With IRV, you rank the candidates. Once all the votes are in, candidates are eliminated one-by-one from the bottom, until someone wins.
That's good news, IRV is a vast improvement over first-past-the-post. Except it is not the best system. It is too complicated -- enough that the UK's tentative to switch to IRV failed, in part because the pro camp couldn't explain it --, it has some trouble spots, and a simpler system performs better.

Check out this fantastic visualization of the differences between the different voting systems. IRV, like first-past-the-post, will sometimes elect someone nobody really wants.

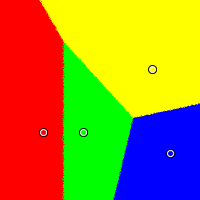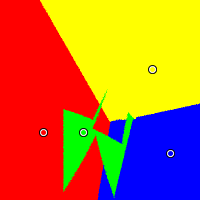Approval Voting

Instant Runoff Voting

In the images, the dots are candidates, and the colored regions around the dot label the range of pooling results which leads to that candidate winning. Under IRV (right-most image), the red, the yellow and the blue candidates all intrude on pooling space that ought to belong to the green candidate.
A better alternative is approval voting: people vote for as many candidates as they want, then the candidates with the most votes wins. It is simpler at the pooling box -- no need to tediously order the candidates -- and vastly simpler to explain.
Here's how things went when I found myself describing these two voting systems (at different times, in different working groups):

---

Approval Voting

-- Vote for however many candidates you want. You can vote for one, for two, for some of them, or for all of them. However you want. The person with the most votes wins.

-- Ok.

---

Instant Runoff Voting

-- Don't worry what IRV means, just list your three favorites candidates. Spot 1 is for your most-favorite candidate (don't be confused, it doesn't mean 'Spot 1 receives 1, points Spot 3 receives 3 points.') When all the votes are in, your vote will go to your #1 candidates. If s/he doesn't win, s/he's out of the race, then we count again, but your vote now goes to your #2 candidates. And so forth, until there is only one candidate left. That person is the winner.

-- What do you mean "And so forth?"

-- I mean it's an algorithm and we had a programmer code it into a computer because the old people who volunteer at poling places sometime don't understand it.

-- confused look. I don't understand. Can you explain it again?

---

That's why I would rather advocate for approval voting. IRV is near impossible to explain to a non-algorithmically-inclined mind. Its opaque name echoes its complicated procedure. And it for all its trouble, it has worse mathematical properties than approval voting.

How to turn a Python loop into a Clojure 'reduce'

This is my answer to this Stack Overflow question.

I wrote a simple stack-based virtual machine in Python, and now I'm trying to rewrite it in Clojure, which is proving difficult as I don't have much experience with Lisp. This Python snippet processes the bytecode, which is represented as a list of tuples like so:

[("label", "entry"),  ("load", 0),  ("load", 1),  ("add",),  ("store", 0)]

pc = 0
for inst in code:
  if inst[0] == "label":
    label = inst[1]
    self.labels[label] = pc
  else:
    self.code.insert(pc, inst)
    pc += 1

I'm going to give you a general solution for these kind of problems.

Most loops can be done effortlessly with a strait forward map, filter or reduce, and if your data structure is recursive, naturally the loop will be a recursion.

Your loop, however, is a different kind of loop. Your loop accumulates a result -- which would suggests using reduce -- but the loop also carries a local variable along (pc), so it's not a strait reduce.

It's a reasonably common kind of loop. If this was Racket, I would use for/fold1, but since it's not, we will have to shoehorn your loop onto reduce.

Let's define a function called load which returns two things, the processed code and the processed labels. I will also use a helper function called is-label?.

(defn load [asm]
  (defn is-label? [x] (= (first x) :label))
  {:code <<< CODE GOES HERE >>>

   :labels
   <<< CODE GOES HERE >>>
  })

Right now, your loop does two things, it processes the code, and it processes the labels. As much as possible, I try to keep loops to a single task. It makes them easier to understand, and it often reveals opportunities for using the simpler loop constructs.

To get the code, we simply need to remove the labels. That's a call to filter.

  {:code (filter (complement is-label?) asm)

   :labels
   <<< CODE GOES HERE >>>
  }

Reduce normally has only one accumulator, but your loop needs two: the result, and the local variablepc. I will package these two into a vector which will be immediately deconstructed by the body of the loop. The two slots of the vector will be my two local variables.

The initial values for these two variables appear as the 2nd argument to reduce.

   (first
    (reduce
     (fn [[result, pc] inst]

        << MORE CODE >>

     [{} 0] asm))

(Note how the initial values for the variables are placed far from their declaration. If the body is long this can be hard to read. That's the problem Racket's for/fold1 solves.)

Once reduce returns, I call first to discard to the local variable pc and keep just the result.

Filling the body of the loop is straight forward. If the instruction is a label, assoc into the result, otherwise increase pc by one. In either case, I construct a vector containing new values for all the local variables.

     (fn [[result, pc] [_ arg :as inst]]
       (if (is-label? inst)
         [(assoc result arg pc) pc]
         [result (inc pc)]))

This technique can be used to convert any accumulator-with-locals loop into a reduce. Here's the full code.

(defn load [asm]
  (defn is-label? [x] (= (first x) :label))
  {:code (filter (complement is-label?) asm)

   :labels
   (first
    (reduce
     (fn [[result, pc] [_ arg :as inst]]
       (if (is-label? inst)
         [(assoc result arg pc) pc]
         [result (inc pc)]))
     [{} 0] asm))})

(println
  (load
   [[:label :entry]
    [:load 0]
    [:load 1]
    [:label :exit]
    [:add]
    [:store 0]]))